- Дискретная случайная величина задана следующим законом распределения:
| 4 | 6 | 10 | 12 | |
| p | 0,4 | 0,1 | 0,2 | 0,3 |
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
- Возможные значения дискретной случайной величины равны: -2, 1, 4. При условии, что заданы математическое ожидание , а также , найти вероятности p1, p2, p3, p4 которые соответствуют дискретным значениям случайной величины.
- Брошены три игральные кости. Найти математическое ожидание суммы квадратов числа очков, которые выпадут на всех гранях.
- Найти закон распределения дискретной случайной величины , которая может принимать только два значения: x1 с вероятностью p1 = 0,1 и x2, причем х1<x2. Математическое ожидание и дисперсия известны: M(X)=3,9, D(X)=0,09.
- Дискретная случайная величина задана законом распределения:
| 3 | 5 | 6 | 9 | |
| p | 0,3 | 0,4 | 0,2 | 0,1 |
Найти функцию распределения F(x) и начертить ее график.
- Дана функция распределения случайной величины
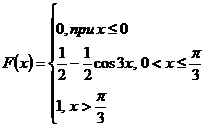
Найти плотность распределения .
- Завод отправил на базу 300 изделий. Вероятность повреждения изделия в пути равна 0,01. Составить ряд распределения числа поврежденных изделий в пути. Воспользоваться законом Пуассона.
- Брак продукции цеха составляет 4%. Определить математическое ожидание и дисперсию числа забракованных изделий из 150 проверенных.
- Интервал движения трамвая 6 минут. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать трамвай менее 4 минут.
- Время ожидания у бензоколонки автозаправочной станции является случайной величиной , распределенной по показательному закону со средним временем ожидания, равным 10 минут. Найти вероятность того, что а) 5мин < <15 мин, б) ≥ 20 мин.
-
- Случайная величина подчиняется нормальному закону распределения с параметрами a = 1, . Определить:
А) Р (-1< <1), Б) Р (0< <3), В) Р (ǀ -1ǀ<0,1).
- Процент выполнения задания (норма выработки) рабочего времени является случайной величиной, подчиненной нормальному закону распределения с математическим ожиданием 110% и средним квадратичным отклонением 2%. Определить вероятность того, что а) выполнение нормы выработки одним рабочим окажется в пределах от 101 до 105% б) выполнение нормы выработки хотя бы одним из трех наудачу взятых рабочих окажется в пределах от 107 до 111%.
