Задание 1

Пусть R(q) = 27N – 2Nq² — доход (выручка) от продажи, а С(q) = q² – 3Nq + 24 -затраты на выпуск продукта в зависимости от количества q. Найти налоговый сбор и величину налога t на каждую единицу продукта, чтобы налоговый сбор Т = tq от всей реализуемой продукции был максимальным. Как уменьшится количество выпускаемой продукции? *

* В качестве N взять последнюю цифру номера зачётной книжки (если цифра 0, то N = 10).

R(q) = 27*6 – 2*6q²=162-12 q²

С(q) = q² – 3*6q + 24= q² – 18q + 24

Задание 2

Решить графическим методом типовую задачу оптимизации. Осуществить проверку правильности решения с помощью средств MS Excel (надстройки Поиск решения) [3]. Номер варианта соответствует последней цифре зачётной книжки.

С графическим методом решения ЗЛП и примерами решения подобных задач можно ознакомиться по учебнику [4], с технологией оптимизации в среде MS Excel – [5].

2.6. Финансовый консультант фирмы «АВС» консультирует клиента по оптимальному инвестиционному портфелю. Клиент хочет вложить средства (не более 25000$) в два наименования акций крупных предприятий в составе холдинга «Дикси». Анализируются акции «Дикси –Е» и «Дикси –В». Цены на акции: «Дикси –Е» — 5$ за акцию; «Дикси –В» — 3$ за акцию. Клиент уточнил, что он хочет приобрести максимум 6000 акций обоих наименований, при этом акций одного из наименований должно быть не более 5000 штук.

По оценкам «АВС» прибыль от инвестиций в эти две акции в следующем году составит: «Дикси –Е» — 1,1$; «Дикси –В» — 0,9$.

Задача консультанта состоит в том, чтобы выдать клиенту рекомендации по оптимизации прибыли от инвестиций.

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум и почему?

Задание 3

В предлагаемой альтернативной хозяйственной ситуации получите с помощью средств MS Excel (надстройка Поиск решения) оптимальный план производства продукции, проведите экономико-математический анализ оптимального плана с помощью двойственных оценок. Номер варианта соответствует последней цифре зачётной книжки.

3.6. На основе информации, приведенной в таблице, решается задача оптимального использования сырья для максимизации выручки от реализации готовой продукции.

Вид сырья	Нормы расхода сырья на единицу продукции			Запасы сырья
	А	Б	В
I	18	15	12	360
II	6	4	8	192
III	5	3	3	180
Цена единицы продукции	9	10	16	—

 

1. Сформулируйте прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получите оптимальный план выпуска продукции.
2. Сформулируйте двойственную задачу и найдите ее оптимальный план (двойственные оценки).
3. Поясните нулевые значения переменных в оптимальном плане.
4. На основе свойств двойственных оценок и теорем двойственности:

а) проанализируйте использование сырья в оптимальном плане

исходной задачи;

б) определите, как изменятся выручка и план выпуска продукции, если запасы сырья первого вида увеличить на 45 единиц, а запасы сырья второго вида уменьшить на 9 единиц;

в) оцените целесообразность включения в план выпуска продукции изделия «Г» ценой 11 единиц, на изготовление которого расходуется 9, 4 и 6 единиц соответствующего вида сырья.

Задание 4

Решить транспортную задачу средствами MS Excel.

На трёх хлебокомбинатах ежедневно производится 46+N₁, 34+N₂, 35+ N₁+N₂ т муки, соответственно. Эта мука потребляется четырьмя хлебозаводами, ежедневные потребности которых равны, соответственно, 40+ N₂, 30+ N₁, 30+ N₁, 20+ N₂ т. Тарифы (в условных единицах) перевозок 1 т муки с хлебокомбинатов к каждому из хлебозаводов задаются матрицей:

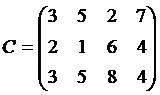
Составить такой план доставки муки, при котором общая стоимость перевозок является минимальной.

N₁ – последняя цифра номера зачётной книжки. N₁=6

N₂ – предпоследняя цифра номера зачётной книжки. N₂=4