Вариант №50
- В партии из 15‑ти изделий есть пять бракованных. Семь наудачу выбранных изделий подвергаются контролю. Найти вероятность того, что среди проверяемых изделий будет обнаружено ровно два бракованных.
- В коробке лежат 12белых и 8 красных шаров, одинаковых на ощупь. Вынули 8 шаров. Какова вероятность того, что красных шаров вынуто не более двух?
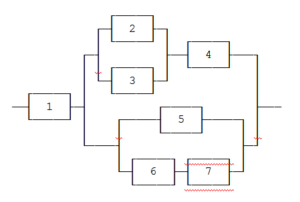
- Найти вероятность надежной работы функциональной цепи, состоящей из независимо работающих элементов, если вероятность выхода из строя каждого элемента одинакова и равна q = 0,3.
- В 4‑х урнах белые и черные шары, одинаковые на ощупь. Впервой —3 белых и 1 черный шар, во второй —6 белых и 4 черных, в третьей —
9 белых и 1 черный, в четвертой —2 белых и 5 черных. Из наудачу выбранной урны случайным образом вынимается один шар. Найти вероятность того, что он белый.
- Вероятность выигрыша по одному билету лотереи равна 1/8. Найти вероятность того, что лицо, имеющее 6билетов, выиграет не более, чем по двум билетам.
- На заводе-автомате 800станков. Вероятность отказа каждого из них 0,1. Найти вероятность того, что в данный момент времени работает не менее 700 станков; ровно 700 станков.
- Вероятность нарушения герметичности баллона равна 0,004. Найти вероятность того, что среди 500баллонов окажется более трех негерметичных баллонов.
- В комплекте 20% нестандартных деталей. Наудачу отобраны четыре детали. Написать закон распределения дискретной случайной величины X‑числа стандартных деталей среди отобранных. Построить многоугольник распределения, вычислить математическое ожидание M(X) и среднее квадратическое отклонение s(X) этого закона и отобразить их на многоугольнике распределения.
- Случайная величина X задана плотностью вероятностей:
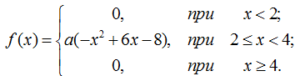
Найти функцию распределения F(x), математическое ожидание M(X), среднее квадратическое отклонение s(X) и вероятность попадания X в интервал (3,5; 3,9). Построить графики плотности и функции распределения и на показать них M(X) и s(X).
- На станке изготавливается деталь. Еедлина X — случайная величина, распределенная по нормальному закону с параметрами: a = 500 см,
s = 1 см. Найти вероятность того, что длина детали заключена между 498 см и 501 см. Какое отклонение длины детали от a можно гарантировать с вероятностью 0,9; 0,99? В каких пределах будут лежать практически все размеры деталей?
- На основе данных о результатах 47‑ми измерений диаметра отливки
| No | D[мм] | No | D[мм] | No | D[мм] | No | D[мм] | No | D[мм] |
| 1 | 144,1 | 11 | 145,0 | 21 | 145,3 | 31 | 145,5 | 41 | 145,9 |
| 2 | 144,4 | 12 | 145,1 | 22 | 145,3 | 32 | 145,5 | 42 | 145,9 |
| 3 | 144,5 | 13 | 145,1 | 23 | 145,4 | 33 | 145,5 | 43 | 145,9 |
| 4 | 144,6 | 14 | 145,1 | 24 | 145,4 | 34 | 145,6 | 44 | 146,0 |
| 5 | 144,7 | 15 | 145,2 | 25 | 145,4 | 35 | 145,6 | 45 | 146,0 |
| 6 | 144,7 | 16 | 145,2 | 26 | 145,4 | 36 | 145,6 | 46 | 146,1 |
| 7 | 144,8 | 17 | 145,2 | 27 | 145,4 | 37 | 145,6 | 47 | 146,2 |
| 8 | 144,9 | 18 | 145,2 | 28 | 145,4 | 38 | 145,7 | ||
| 9 | 144,9 | 19 | 145,3 | 29 | 145,4 | 39 | 145,7 | ||
| 10 | 144,9 | 20 | 145,3 | 30 | 145,5 | 40 | 145,7 |
сформировать таблицу значений относительных частот для равноотстоящих вариант, таблицу значений эмпирической плотности относительных частот и эмпирической функции распределения, разбив рассматриваемый отрезок значений исследуемого параметра на 8 равноотстоящих частичных интервалов.
- Построить полигон и гистограмму относительных частот и график эмпирической функции распределения.
- Вычислить выборочную среднюю выборки, её дисперсию, выборочное среднее квадратическое отклонение и выборочные коэффициенты асимметрии и эксцесса, отобразив выборочную среднюю и выборочное среднее квадратическое отклонение на полигоне и гистограмме относительных частот.
- Найти точечные оценки параметров нормального закона распределения, записать соответствующую формулу для плотности вероятностей f(x) и рассчитать теоретические относительные частоты. Построить график плотности распределения на гистограмме относительных частот, а теоретические относительные частоты показать на полигоне относительных частот.
- Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность g = 0,95и 0,99.
- Проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0,01; 0,05.
- Найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы
nij
X 50 55 60 65 70 Y 30 5 5 40 6 4 50 40 15 60 5 10 70 5 80 2 3
