Часть 1. Методы элементарной математики
ЗАДАЧА 1: Кредит в сумме k руб. выдан на n лет по ставке v % годовых с равномерным ежегодным погашением. Определить размеры ежегодных выплат и сумму уплачиваемых процентов, если платежи осуществляются поквартально.
| Номер варианта | Сумма кредита,
руб (a) |
Срок кредита,
лет (n) |
Процентная ставка,
% в год (v) |
| 3 | 15000 | 5 | 16 |
ЗАДАЧА 2: Пусть долг равен m руб. и выдан под z% годовых. Для погашения долга предполагается выделять сумму порядка s руб. в год. Оценить величину срока, необходимого для погашения задолженности.
| Номер варианта | Сумма долга,
руб (m) |
Процентная ставка,
% в год (z) |
Предполагаемая сумма погашения в год, (s) |
| 3 | 15000 | 16 | 5000 |
ЗАДАЧА 3: Долг в размере Q руб. решено погасить по специальному графику за 4 года – размеры расходов по погашению долга по годам: m, n и k. Остаток выплачивается в конце четвертого года. План ежемесячного погашения составьте при условии, что ставка процента по долгу составляет z% в год
| Номер варианта | Сумма долга,
руб (Q) |
Предполагаемая сумма погашения в 1 год, (m) | Предполагаемая сумма погашения вo 2 год, (n) | Предполагаемая сумма погашения в 3 год, (k) | Процентная
ставка, % в год (z) |
| 3 | 15000 | 4500 | 3000 | 5000 | 16 |
Часть 2. Методы и модели математической статистики
Задача 4. По данным таблицы 1.N произвести группировку заводов по производству продукции за отчетный период, образовав пять групп заводов. Каждую группу охарактеризуйте числом заводов, числом работающих, среднегодовой стоимостью ОПФ. Наряду с абсолютными показателями по группам, вычислить их процентное соотношение. Сделать выводы.
Табл.1.4
| Номер п/п | Среднегодовая стоимость ОПФ, млн. руб. | Среднесписочное число работающих за отчетный период, чел. | Производство продукции за отчетный период, млн. р | Выполнение плана, % |
| 1 | 3,5 | 88 | 14,5 | 109,5 |
| 2 | 2,6 | 94 | 7,9 | 112,9 |
| 3 | 9,0 | 70 | 4,6 | 97,8 |
| 4 | 2,8 | 142 | 12,1 | 106,3 |
| 5 | 3,1 | 144 | 11 | 105,5 |
| 6 | 4,8 | 83 | 9,2 | 112,4 |
| 7 | 5,7 | 104 | 13 | 101,4 |
| 8 | 7,3 | 56 | 15,3 | 94,1 |
| 9 | 2,1 | 70 | 1,3 | 110,6 |
| 10 | 4,6 | 100 | 3,1 | 96,3 |
| 11 | 1,9 | 82 | 2 | 98 |
| 12 | 3,8 | 105 | 1 | 105,2 |
| 13 | 5,9 | 116 | 10,9 | 100,3 |
| 14 | 8,9 | 51 | 19,1 | 103,6 |
| 15 | 4,1 | 140 | 4,5 | 111,4 |
| 16 | 4,3 | 51 | 6,9 | 103,9 |
| 17 | 1,4 | 152 | 17,8 | 112,2 |
| 18 | 3,8 | 72 | 9,6 | 108,3 |
| 19 | 3,4 | 69 | 4,6 | 101,1 |
| 20 | 0,7 | 100 | 17 | 108,1 |
| 21 | 4,0 | 89 | 1,4 | 104,5 |
| 22 | 9,1 | 70 | 2,7 | 101,9 |
| 23 | 8,3 | 116 | 19,3 | 93,9 |
| 24 | 7,1 | 156 | 16,7 | 93,8 |
| Итого | 112,9 | 2320 | 225,7 |
ЗАДАЧА5. Исследовать характер изменения с течением времени уровня производства мяса и валового сбора зерна располагая статистическими данными, приведенными в таблице 2.N. Построить уравнения регрессии 1, 2 и 3 порядка для этих данных. Сравнить полученные результаты, сделать выводы.
Таблица 2.4
Данные по производству мяса и зерна в России
| Год | 2003 | 2004 | 2005 | 2006 | 2007 |
| Валовой сбор зерна (млн.т.) | 157,42 | 101,03 | 183,39 | 135,93 | 181,88 |
| Производство мяса (млн.т.) | 20,524 | 21,159 | 14,648 | 18,85 | 13,897 |
ЧАСТЬ 3. Элементы анализа
Задача 6. Исследовать на выпуклость функции f(х), вида ![]()
полученные в результате решения задачи 5, как квадратичная зависимость (уравнение регресии второго порядка ).
ЗАДАЧА 7. Объем продукции , произведенной бригадой рабочих, может быть описан уравнением
![]()
где — рабочее время в часах, k,l,m,n – коэффициенты уравнения, выбираемые в соответствии со своим вариантом из таблицы.
Вычислить производительность труда, скорость и темп ее изменения через час после начала работы и за час до ее окончания.
| Номер варианта | k | m | n | l |
| 3 | 1/7 | 4/3 | 30 | 34 |
ЗАДАЧА 8. Пусть функция затрат имеет вид:
![]()
Определить предельные издержки производства при данном объеме выпуска х1 и х2.
Значения Z,W, х1 и х2 выбрать из таблицы согласно варианту.
| Номер варианта | Z | W | X1 | X2 |
| 3 | 1 | 3 | 3 | 10 |
ЗАДАЧА 9. Пусть зависимость спроса на товар от цены на него выражается формулой 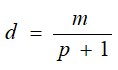 . Определим скорость изменения спроса, когда цена на товар составляет p1 ден.ед., p2 ден. ед.
. Определим скорость изменения спроса, когда цена на товар составляет p1 ден.ед., p2 ден. ед.
| Номер варианта | m | P1 | P2 |
| 3 | 100 | 3 | 9 |
ЗАДАЧА 10
По плану производства продукции предприятию необходимо изготовить m изделий. Эти изделия могут быть изготовлены 2-мя технологическими способами. При производстве — изделий 1-ым способом затраты равны (т. руб.), а при изготовлении — изделий 2-ым способом они составят (т. руб.).
Определить сколько изделий каждым из способов необходимо изготовить, чтобы общие затраты на производство были минимальные.
| Номер варианта | m | n | k |
| 3 | 100 | 3 | 9 |
