Эконометрика вариант 6

Задания по теме «Парная регрессия».

 

Экономический смысл параметров

 

Задание 1. Для функции вида   определить прогнозное значение .

— текущее значение ,  — прогнозное значение ,  — текущее значение ,

— прогнозное значение

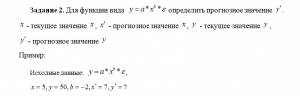
Задание 3. Определить параметры линейной регрессии:

а) с помощью системы нормальных уравнений;

б) по расчетной формуле;

в) в матричной форме.

г) записать уравнение регрессии с найденными параметрами.

Задание 4. Привести нелинейную регрессию к линейному виду:

Пример:

Исходные данные:

Задание 7. Для функции вида   определить значение критерия Фишера, при

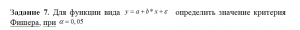
Пример:

Исходные данные:

TSS =100, ESS = 99, RSS = 1, n= 21, m =2.

Задание 8. Для функции вида   определить значение критерия Стьюдента, при

а) Найти стандартизированную ошибки коэффициентов регрессии;

б) найти значение критерия Стьюдента для всех переменных;

в) сделать вывод о значимости параметров регрессии.

Задание 9. Для функции вида

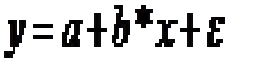
рассчитать доверительные интервалы для параметров.

Исходные данные:

а = 20, b = 15, m_a = 8,083, m_b = 2,582, t_a = 2,474 , t_b = 5,809.

Задание 10. Для функции вида   определить интервальный прогноз на основе линейного уравнения регрессии

Исходные данные:   =3, Σ(Х — )² = 10 , n=3, RSS = 200

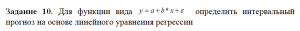
Задание 11.  Найти частные уравнения множественной регрессии.

Пример:

Исходные данные:  y = 20+5*x₁+3*x₂ , х₁ ср = 7 , х₂ ср  = 5.

Задание 12. Найти уравнение регрессии в стандартизированном масштабе

Исходные данные:  r_yx1 = 0,9 , r_yx2 = 0,7 , r_x1x2 = 0,1, σ_x1 = 47, σ_x2 =300 , σ_y = 15, у _ср = 15, х_{1 ср} =7 , х_{2 ср} = 3.

Задание 13. Найти индекс множественной корреляции

Исходные данные:  TSS = 10000, ESS = 9000, RSS = 1000, n=7

Задание 14. Найти средний показатель эластичности:

Исходные данные: у_ср = 15, х _ср =17 , b = 2.

Задание 15. Провести сглаживание ряда методом скользящей средней

Задание 16. Известно уравнение тренда и значения сезонной компоненты, определить значение Y по аддитивной модели в периоде t.

Уравнение тренда Т= 12+3*t.

№	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12
Значение сезонной компоненты	1	3	5	3	1	-1	-3	-5	-3	-1	1	3

t = 45

Задание 17. Провести идентификацию системы уравнений.

Исходные данные:

Вариант 6.

y₁=b₁₂y₂+b₁₃y₃+a₁₃x₃

y₂=b₂₃y₃+b₂₃y₃+a₂₂x₂

y₃=b₃₁y₁+a₃₁x₁+a₃₃x₃

Задание 18. Найти структурные коэффициенты системы уравнений, исходя из приведённой формы модели.

 

Исходные данные:

y₁=b₁₂y₂+a₁₂x₂+a₁₃x₃

y₂=b₂₃y₃+a₂₂x₂+a₂₃x₃

y₃=b₃₁y₁+a₃₂x₂+a₃₃x₃

коэффициенты системы уравнений в приведённой форме:

3; 4; 10

2; -5; 2

-6; 8; 5